Binary v/s Decimal number

Understanding binary and decimal numbers is fundamental in mathematics and computer science. This guide will cover the basics of both number systems and provide step-by-step methods to convert between decimal and binary.

---

Understanding Binary and Decimal Numbers

1. Decimal Number System (Base-10)

The decimal number system, also known as Base-10, is the system we use in everyday life. It consists of ten digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.

Each digit's position in a number determines its value based on powers of 10.
For example, in the decimal number 523, the value is calculated as:

523 = (5 \times 10^2) + (2 \times 10^1) + (3 \times 10^0)

= (5 \times 100) + (2 \times 10) + (3 \times 1) ]

= 500 + 20 + 3 = 523

Characteristics of Decimal System

• Uses ten digits (0-9).
• Each place value represents a power of 10.
• Used in daily calculations.

---

2. Binary Number System (Base-2)

The binary number system, or Base-2, is used in computers and digital systems. It consists of only two digits:
0 and 1.

Each digit’s position in a binary number is based on powers of 2.
For example, in the binary number 1011, the value is calculated as:

1011 = (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (1 \times 2^0)

= (1 \times 8) + (0 \times 4) + (1 \times 2) + (1 \times 1) ]

= 8 + 0 + 2 + 1 = 11 \text{ (Decimal)}

Characteristics of Binary System

• Uses only two digits (0 and 1).
• Each place value represents a power of 2.
• Used in computers and electronic systems.

---

Conversion Methods

3. Converting Decimal to Binary

To convert a decimal number to binary, use repeated division by 2 and record the remainders.

Steps to Convert Decimal to Binary

1. Divide the decimal number by 2.
2. Write down the remainder.
3. Continue dividing the quotient by 2 until you reach 0.
4. The binary equivalent is the remainders read in reverse order.

Example 1: Convert 19 (Decimal) to Binary

1. remainder 1
2. remainder 1
3. remainder 0
4. remainder 0
5. remainder 1

Reading from bottom to top:
19 (Decimal) = 10011 (Binary)

---

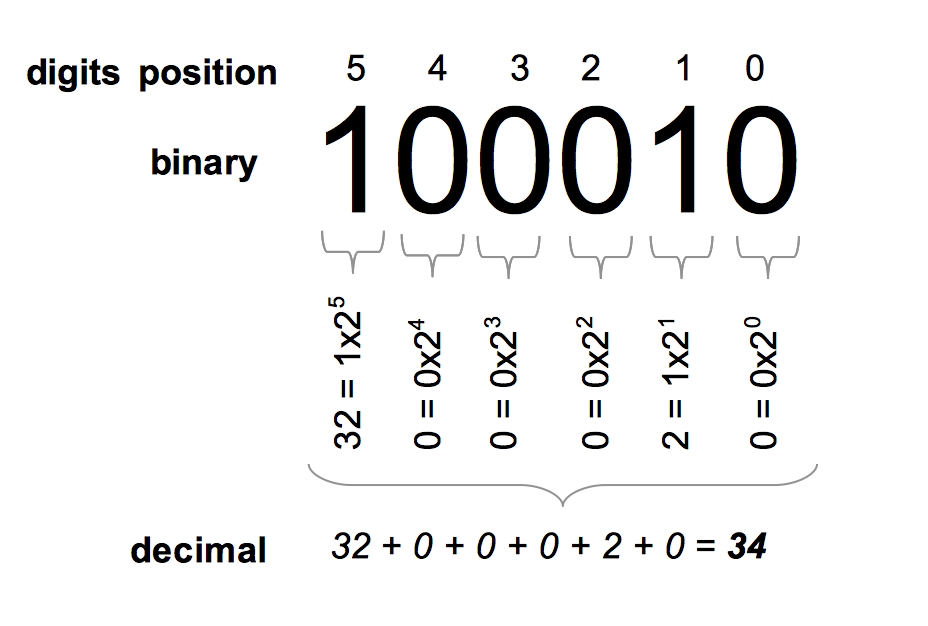
4. Converting Binary to Decimal

To convert a binary number to decimal, use the weighted sum of powers of 2.

Steps to Convert Binary to Decimal

1. Write the binary number.
2. Multiply each digit by powers of 2, starting from 0 on the right.
3. Sum up all the values.

Example 2: Convert 1010 (Binary) to Decimal

1010 = (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0)

= (1 \times 8) + (0 \times 4) + (1 \times 2) + (0 \times 1) ]

= 8 + 0 + 2 + 0 = 10

1010 (Binary) = 10 (Decimal)

---

5. Converting Decimal to Binary Using the Subtraction Method

Instead of division, another method involves subtracting the largest power of 2 until reaching 0.

Steps

1. Find the largest power of 2 within the decimal number.
2. Subtract it from the number and record "1" at that place.
3. If a power of 2 is not used, record "0".
4. Repeat until reaching 0.

Example 3: Convert 13 (Decimal) to Binary

1. Largest power of 2 ≤ 13 is 8 (2³).
   13 - 8 = 5 → 1
2. Largest power of 2 ≤ 5 is 4 (2²).
   5 - 4 = 1 → 1
3. Largest power of 2 ≤ 1 is 1 (2⁰).
   1 - 1 = 0 → 1

Binary representation (using powers of 2): 1101
13 (Decimal) = 1101 (Binary)

---

6. Converting Binary to Decimal Using Doubling Method

Another approach for binary-to-decimal conversion is doubling.

Steps

1. Start with 0.
2. Double the result and add the next binary digit.
3. Continue until all digits are processed.

Example 4: Convert 1101 (Binary) to Decimal

1. Start with 0

1101 (Binary) = 13 (Decimal)

---

7. Converting Fractional Decimal to Binary

For fractional decimal numbers, use multiplication by 2.

Steps

1. Multiply the fractional part by 2.
2. Record the integer part (0 or 1).
3. Repeat with the fractional remainder.
4. Stop when the fraction becomes 0 (or after enough decimal places).

Example 5: Convert 0.625 (Decimal) to Binary

1. → 1
2. → 0
3. → 1

0.625 (Decimal) = 0.101 (Binary)

---

8. Converting Fractional Binary to Decimal

Multiply each digit by negative powers of 2.

Example 6: Convert 0.101 (Binary) to Decimal

(1 \times 2^{-1}) + (0 \times 2^{-2}) + (1 \times 2^{-3})

(1 \times 0.5) + (0 \times 0.25) + (1 \times 0.125) ]

0.5 + 0 + 0.125 = 0.625

0.101 (Binary) = 0.625 (Decimal)

---

Conclusion

Understanding binary and decimal numbers is essential for computing. The division-remainder method is best for converting decimal to binary, while the weighted sum method works for binary to decimal. These conversions are the foundation of digital computing and number systems.